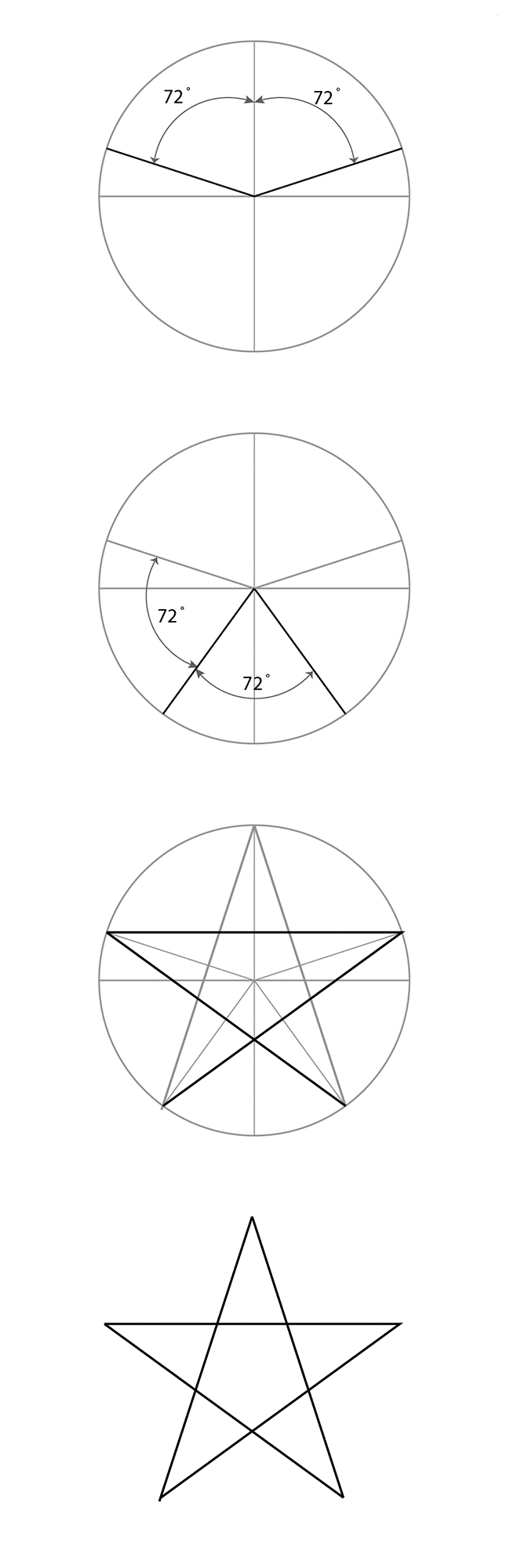
Como desenhar um círculo?

Então, vamos começar o tópico de hoje com uma situação de vida: como desenhar um círculo, se não há bússola? Não importa, você pode fazer sem ele!

Instruções passo a passo

• Pegue uma folha de papel em uma caixa, conte deSeu limite superior de 6 células é a linha do centro do círculo. Na linha central a partir da borda esquerda da folha, deixe-nos recuar 7 células - este é o centro. Do centro, nós avançamos em 5 células e chegamos ao ponto mais alto do nosso círculo (A). E, em seguida, aplique um foco pequeno, incluído em 3 pares de dígitos: 3.1; 1.1; 1.3.
• Se você começar com A, você pode obter o seguinteponto do círculo (B), passando 3 células para a direita e 1 para baixo (o primeiro par de dígitos), da célula B - 1 para a direita e 1 para baixo (o segundo par e ponto Z) e de Z para 1 célula para a direita e 3 para baixo D).
• Gire a folha 90 ° no sentido anti-horário,tornando D o ponto mais alto e repita os mesmos 6 passos. Novamente, gire a folha 90 ° no sentido anti-horário, encontre os novos 3 pontos. Na terceira vez, gire a folha e siga os mesmos três pares de números.
• Conectando com precisão a curva suave obtida com a ajuda de nossos pontos de foco, obtemos o resultado desejado. É assim que desenhar um círculo sem uma bússola!

Uma nova tarefa: é necessário desenhar uma projeção axonométrica do círculo.

Projeção axonométrica de um círculo

Desenhe um círculo e, em seguida, para obternecessário na construção de sua projeção paralela de pontos, vamos inscrevê-lo em um quadrado, colocando-o horizontalmente. Os lados do quadrado são tangentes ao círculo. Denote os pontos de tangência (o meio dos lados do quadrado). Desenho das diagonais da praça, recebemos mais 4 pontos nos lugares de sua interseção com o círculo. Vale ressaltar que esses pontos dividem cada parte de sua semi-diagonal em 2 partes com uma proporção de 3: 7.

Construímos o plano para o qual queremosexiba nosso círculo. Agora desenhe linhas paralelas entre si através dos vértices do quadrado até se cruzarem com este plano. Os pontos resultantes tornam-se os vértices da projeção axonométrica do quadrado que descreve o círculo - o paralelogramo. Vamos desenhar essa figura e suas diagonais. A interseção das diagonais é o mapeamento do centro do nosso círculo.

Agora vamos descobrir como desenhar um círculo emaxonometria, aplicando seu teorema principal. Vamos encontrar o meio de cada lado do paralelogramo. Desenhe linhas retas paralelas desenhadas a partir dos vértices do quadrado através dos pontos localizados nas diagonais antes da sua interseção com as diagonais do paralelogramo. Tendo conectado os pontos de uma curva suave obtida com projeção paralela, obtemos uma elipse - a projeção do círculo no plano.

Círculo em isometria

Vamos complicar a tarefa e tentar entender como desenharcircunferência na isometria. Uma vez que a isometria é uma projeção axonométrica retangular padrão, como resultado, novamente obtemos projeções sob a forma de elipses. Nós tomamos o diâmetro do círculo original para ser d. Se a projeção isométrica for construída sem contração ao longo dos eixos de coordenadas, conforme indicado em GOST 2.317-69, o grande eixo de cada uma das 3 elipses é 1.22d, enquanto os pequenos eixos das elipses dos planos dispostos verticalmente são 0.35d e o eixo menor da terceira elipse é 0,95d. Isometricamente, os pequenos eixos das três elipses correspondem a 0,58d, e a posição dos eixos de coordenadas é a seguinte: os eixos X e Y estão localizados à esquerda e à direita do eixo Z em um ângulo de 120 °.

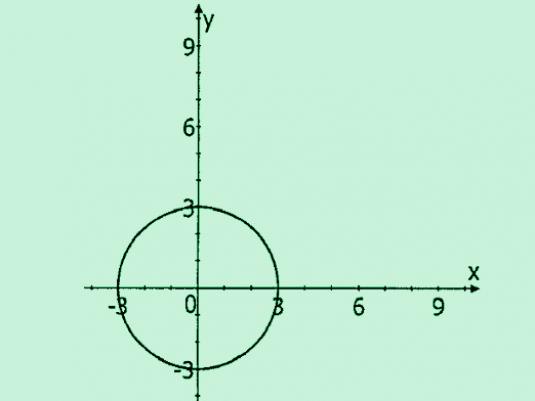
Compreenda como desenhar um círculo dadoequação, podemos facilmente ajudar a equação do círculo em si. Mostra quais coordenadas têm o centro do círculo e qual é o raio do círculo. Então, só resta tirar e desenhar.